PyTorch 입문3

[0] 참고자료

• PyTorch로 시작하는 딥 러닝 입문 유원준 외 1명
• 딥러닝 파이토치 교과서 서지영

[7] 인공 신경망2

1. 역전파 BackPropagation

1. Sample Model

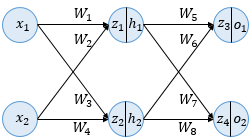
• 입력층, 은닉층1, 출력층
• 각 층은 2개의 뉴런 사용
• 은닉층과 출력층은 활성화 함수로 시그모이드 사용

1. 순전파 Forward Propagation

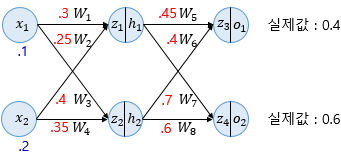
• 은닉층
  • z1 = x1 * W1 + x2 * W2 = 0.30.1 + 0.250.2 = 0.08
  • z2 = x1 * W3 + x2 * W4 = 0.30.4 + 0.350.2 = 0.11
• 은닉층 시그모이드
  • h1 = sigmoid(z1) = 0.51998934
  • h2 = sigmoid(z2) = 0.52747230
• 출력층
  • z3 = h1 * W5 + h2 * W6 = h1 * 0.45 + h2 * 0.4 = 0.44498412
  • z4 = h1 * W7 + h2 * W8 = h1 * 0.7 + h2 * 0.6 = 0.68047592
• 은닉층 시그모이드
  • o1 = sigmoid(z3) = 0.60944600
  • o2 = sigmoid(z4) = 0.66384491
• 오차
  • E = 1/2 * (targeto1 - outputo1)^2 + 1/2 * (targeto2 - outputo2)^2
  • E = 1/2 * (0.4 - 0.60944600)^2 + 1/2 * (0.6 - 0.66384491)^2 = 0.02397190

1. 역전파 Sample

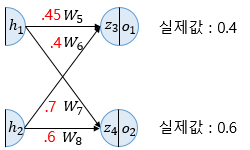
• 출력층과 은닉층 사이의 가중치 W5, W6, W7, W8을 업데이트 한다.
• W5 업데이트
  • 경사 하강법을 통해 업데이트
  • W5+ = W5 - α*(θE/θW5)
  • θE/θW5 = θE/θo1 * θo1/θz3 * θz3/θW5
• θE/θo1
  • Error 값을 o1에 대해 미분
  • θE/θo1 = 2 * 1/2 * (targeto1 - outputo1)^(2 - 1) * (-1) + 0
  • θE/θo1 = - (targeto1 - outputo1) = - (0.4 - 0.60944600) = 0.20944600
• θo1/θz3
  • o1은 시그모이드 함수의 출력값
  • 시그모이드 함수의 미분은 f(x)*(1 - f(x)).
  • θo1/θz3 = o1 * (1 - o1) = 0.60944600 * (1 - 0.60944600) = 0.23802157
• θz3/θW5
  • θz3/θW5 = h1 = 0.51998934
• θE/θW5 = θE/θo1 * θo1/θz3 * θz3/θW5
  • 0.20944600 * 0.23802157 * 0.51998934 = 0.02592286
• W5+ = W5 - α*(θE/θW5)
  • α 는 learning rate 0.5라고 가정
  • 0.45 - 0.5 * 0.02592286 = 0.43703857

2. 비선형 활성화 함수 Activation function

• 입력을 받아 수학적 변환을 수행하고 출력을 생성하는 함수
• ex) sigmoid, softmax

1. 특징
   • 비선형 함수 Nonlinear function
     • 직선 1개로는 그릴 수 없는 함수
     • 활성화함수로 선형 함수를 선택하고 layer를 추가하는 경우,
     • 활성화 함수 f(x) = Wx
     • 은닉층을 추가하면 y(x) = f((fx)) = W1W2x = kx
     • 즉, 은닉층을 여러번 추가해도 차이가 없음
     • 활성화함수로 선형 함수를 주는 경우는 가중치의 변화를 좀 더 주고 싶은 경우
     • 일반적으로는 비선형함수를 선택함
2. 시그모이드 함수와 기울기 소실

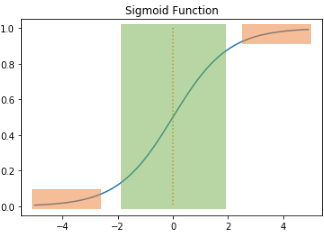
• 시그모이드의 출력값이 0 또는 1에 가까워지면, 그래프의 기울기가 0에 가까워짐

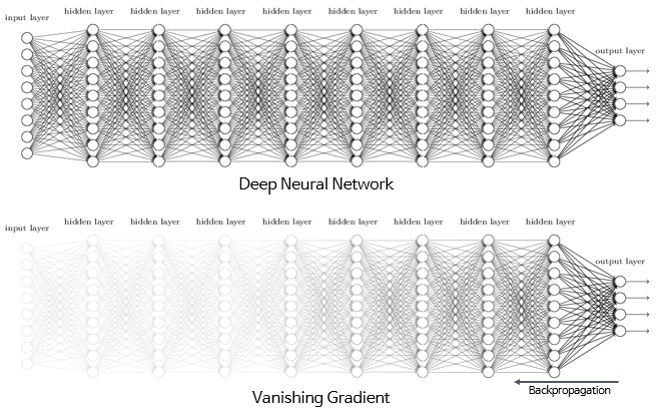
• 역전파 과정에서 기울기(미분)을 사용하게 되는데, 이 때 기울기가 0에 가까워지면 앞단에 전달되지 않음
• 따라서 시그모이드 함수를 은닉층에 사용할 때는 어려움이 있음

1. 하이퍼볼릭탄젠트 함수 Hyperbolic tangent function

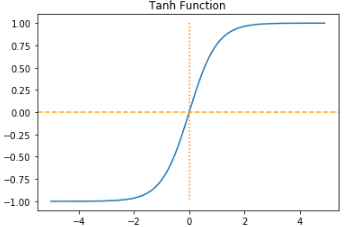
• 입력값을 -1과 1 사이로 변환함
• 양 끝 기울기가 0에 가까워지는 문제는 시그모이드와 같음
• 0을 중심으로 하기때문에 시그모이드 함수보다는 기울기 소실 증상이 적은 편임

1. 렐루 함수 ReLU

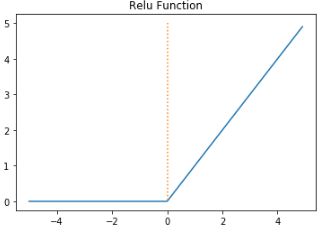
• 음수를 입력하면 0, 양수를 입력하면 그대로 반환
  • f(x) = max(0, x)
• 특정 값에 수렴하지 않으므로 시그모이드보다 잘 작동함
• 시그모이드, 하이퍼볼릭탄젠트와 같이 연산이 필요한 것이 아니므로 연산 속도가 빠름
• 입력값이 음수면 기울기도 0이 되는 것이 단점 - dying ReLU

1. Leaky ReLU
   • 렐루를 보완하기 위한 방법 중 하나
   • 입력값이 음수인 경우 0.001과 같은 매우 작은 수를 반환
2. Softmax function
   • 출력층에 적용할 수 있음

[8] 합성곱 신경망 CNN Convolutional Neural Network

1. Why Convolution?

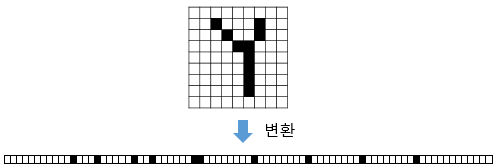
• 이미지 데이터를 입력으로 주면 결국 1차원 데이터가 되는데, 변환 전의 공간적인 구조 정보가 유실됨
• 공간적인 구조 정보 : 거리가 가까운 픽셀간의 관계

2. Channel

• 이미지는 (높이 x 너비 x 채널) 이라는 3차원 텐서
• 높이 : 세로 방향 픽셀 수
• 너비 : 가로 방향 픽셀 수
• 채널 : 색 성분. 흑백은 1채널, 일반적인 컬러는 3채널

3. Convolution opertation

• 합성곱층은 이미지의 특징을 추출하는 역할
• 커널(kernel) 또는 필터(filter)라는 n x m 크기의 행렬로 이미지를 처음부터 끝까지 훑으면서 출력값을 생성함
• 커널은 일반적으로 3 x 3 또는 5 x 5를 사용함

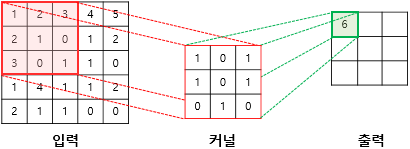
(1×1) + (2×0) + (3×1) + (2×1) + (1×0) + (0×1) + (3×0) + (0×1) + (1×0) = 6

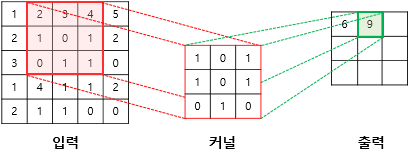
(2×1) + (3×0) + (4×1) + (1×1) + (0×0) + (1×1) + (0×0) + (1×1) + (1×0) = 9

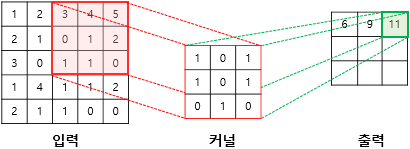
(3×1) + (4×0) + (5×1) + (0×1) + (1×0) + (2×1) + (1×0) + (1×1) + (0×0) = 11

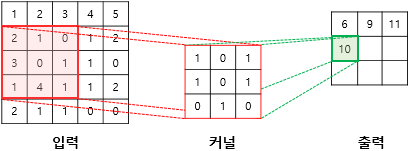
(2×1) + (1×0) + (0×1) + (3×1) + (0×0) + (1×1) + (1×0) + (4×1) + (1×0) = 10

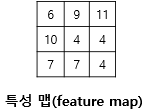
• 입력과 커널의 합성곱으로 나온 결과를 특성 맵이라 함
• 커널의 크기, 이동범위(stride)는 사용자가 지정 가능
• 5 x 5 이미지에 3 x 3 커널 2스트라이드인 경우

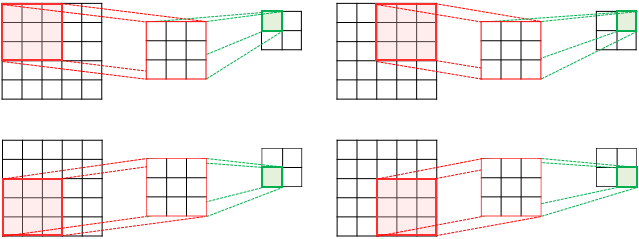
4. Padding

• 특성맵은 입력보다 크기가 작아진다는 단점이 있음
• 합성곱 층이 여러 개인 경우, 특성 맵의 크기가 너무 작아질 수 있음
• 합성곱 연산 전에 입력의 가장자리에 행과 열을 추가해주는 방법

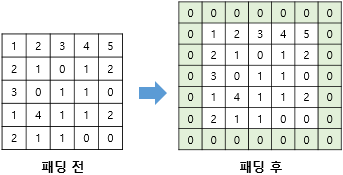
5. Multi-Channel Convolution

• 실제 합성곱 연산의 입력은 다수의 채널을 가진 이미지 또는 이전 연산의 결과일 수 있음
• 따라서 합성곱 연산시에는 커널의 채널 수 또한 입력 채널 수와 같아야 함

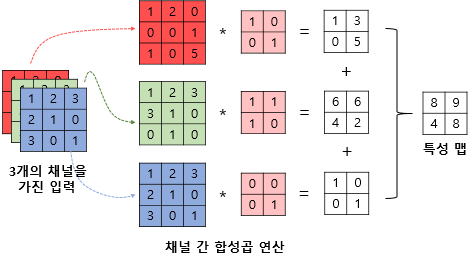
6. CNN MNIST

import torch
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import torch.nn as nn
import torch.nn.init
from torch.utils.data import DataLoader


device = 'cuda' if torch.cuda.is_available() else 'cpu'

torch.manual_seed(777)

if device == 'cuda':
    torch.cuda.manual_seed_all(777)

learning_rate = 0.001
trainint_epochs = 15
batch_size = 100

mnist_train = dsets.MNIST(root='MNIST_data/',
                            train=True,
                            transform=transforms.ToTensor(),
                            download=True)

mnist_test = dsets.MNIST(root='MNIST_data/',
                            train=False,
                            transform=transforms.ToTensor(),
                            download=True)

data_loader = DataLoader(dataset=mnist_train,
                        batch_size=batch_size,
                        shuffle=True,
                        drop_last=True)


class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        # 첫번째층
        # ImgIn shape=(?, 28, 28, 1)
        #    Conv     -> (?, 28, 28, 32)
        #    Pool     -> (?, 14, 14, 32)
        self.layer1 = nn.Sequential(
            nn.Conv2d(1, 32, kernel_size=3, stride=1, padding=1),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2, stride=2)
        )

        # 두번째층
        # ImgIn shape=(?, 14, 14, 32)
        #    Conv      ->(?, 14, 14, 64)
        #    Pool      ->(?, 7, 7, 64)
        self.layer2 = nn.Sequential(
            nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2, stride=2)
        )

        # 전결합층 7x7x64 inputs -> 10 outputs
        self.fc = torch.nn.Linear(7 * 7 * 64, 10, bias=True)

        # 전결합층 한정으로 가중치 초기화
        nn.init.xavier_uniform_(self.fc.weight)

    def forward(self, x):
        out = self.layer1(x)
        out = self.layer2(out)
        out = out.view(out.size(0), -1)
        out = self.fc(out)
        return out


model = CNN().to(device)
criterion = nn.CrossEntropyLoss().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

total_batch = len(data_loader)
print('총 배치의 수 : {}'.format(total_batch))

for epoch in range(trainint_epochs):
    avg_cost = 0

    for X, Y in data_loader:
        # image is already size of (28 x 28), no reshpae
        # label is not one-hot encoded
        X = X.to(device)
        Y = Y.to(device)

        optimizer.zero_grad()
        hypothesis = model(X)
        cost = criterion(hypothesis, Y)
        cost.backward()
        optimizer.step()

        avg_cost += cost / total_batch

    print('[Epoch: {:>4}] cost = {:>.9}'.format(epoch + 1, avg_cost))

with torch.no_grad():
    X_test = mnist_test.data.view(len(mnist_test), 1, 28, 28).float().to(device)
    Y_test = mnist_test.targets.to(device)

    prediction = model(X_test)
    correct_prediction = model(X_test)
    correct_prediction = torch.argmax(prediction, 1) == Y_test
    accuracy = correct_prediction.float().mean()
    print('Accuracy: ', accuracy.item())